SETS,
RELATION AND FUNCTIONS
DEFINITION OF A SET:
A well defined collection of distinct objects is
called a SET.
The members of a set are called its ELEMENTS.
The sets are generally denoted by capital letters
A, B, C...., X, Y, Z.
The elements of a set are generally denoted by small letters a, b, c,....., x,
y, z.
If x is an element of the set A, we write x∈A
If x is not an element of the set A, we write as
A well defined collection is such that given an
object, it is possible to determine whether the object belongs to the
particular collection or net, for example, the collection of all officers in
the Post office, the collection of all subject taught to
students of class X, collection of all IT companies.
On the other hand, the collection of all intelligent
students in a class, the collection of all tall girls in a senior secondary
school, the collection of all difficult questions asked in Mathematics, Physics
and Chemistry in NEET 21 are not sets, since the words intelligent, tall,
difficult are not well defined.
DESCRIPTION OF A SET
A set can be represented by either of the following
two methods :
ROSTER METHOD OR TABULAR FORM
In this method a set is represented by listing all
its elements separated by commas within {} For example,
· The set V of vowels in English alphabet
is V = {a, e, i, o, u}
· The set E of even natural numbers is E
= {2, 4, 6, 8,......}
· The set of letters forming the word
SCHOOL is {S, C, H, O, L}
PROPERTY METHOD OR SET BUILDER
FORM
In this method, a, set is represented by stating a
rule or a set of rules, which are satisfied by all the elements of the set and
not by any other element outside the set. In general, we write S = { x : P (x)}
Which means that S is a set of elements, which
satisfy the condition P(x).
[The symbol : or | is read as “such that”]
For example
V = { x : x is a vowel in the English alphabet}
E = {x : x is an even natural number}
A = { x : x is a letter of the word SCHOOL}
B = {x : x is a factor of 40, x ∈ N} = {1, 2, 4, 5, 8, 10, 20, 40}
TYPES OF SET
1. EMPTY SET OR NULL SET OR VOID SET
A set which does not contain any element is called
the empty set.
A null set is denoted by φ or {}.
For example:
- C = {x : x is an even prime number
greater than 2}
- D = {x : x is a married bachelor}
2. SINGLETON SET
A set containing only one element is called a
singleton set.
For example:
- A = {4}.
- C = {a}.
- D = { x : x+4 = 0, x∈I}.
- {0} is a singleton set.
- φ is a void set but {φ} is a singleton
set.
3. FINITE AND INFINITE SETS
A set which is empty or consists of a definite
number of elements is called FINITE. If a set A consists of n distinct
elements then we write n (A) = n or O (A) = n It is called the CARDINAL
NUMBER, or CARDINALITY or ORDER of the set A. The cardinality
of a void set is zero and the cardinality of a singleton set is 1. Other
examples of finite set, are
- Set A of days of the week, n (A) = 7
- Set V of vowels in English alphabet,
n(V) = 5
- Set M of all men is the
world, n (M) may be a quite big number but it is a finite number although we do
not know the exact number of elements in M.
INFINITE SET
A set whose elements cannot
be counted is called an INFINITE SET.
For example,
N : the set of natural number = { 1,2,3.........}
Z or I : the set of integers = { ......., –3, –2,
–1, 0, 1, 2, 3,....}
R+ : the set of positive real numbers
Q+ : the set of positive rational
numbers
I+ : the set of positive integers
4. EQUAL AND EQUIVALENT SETS
Given two sets A and B. If every element of A is
also an element of B and vice versa, the sets A and B are said to be equal and
we write A = B. Clearly, A = B, if they have exactly the same elements.
(The symbol '⇒' stands for 'implies that')
For example:
- Let A ={1, 4, 5} and B = {4, 1, 5},
then A = B
- Let A = { x : 2 x 6, } and B =
{2, 3, 4, 5, 6} then A = B
- Let A = { x : x is a prime number
number less than 6} and B = {x : x is a prime factor of 30}, then A = B
- Let A = { x : x is a letter of the word
ALLOY} and B = {x : x is a letter of the word LOYAL} then A = B
- Let A = {1, 2}, B = {1, 2, 2, 1} and C
= { x : x2 – 3x + 2=0} then A = B = C.
Two finite sets A and B are said to be EQUIVALENT
if they have the same number of elements, i.e. n(A) = n(B). We write A≈B
All equal sets are equivalent but all equivalent sets are not equal.
For example:
- A = {a, b, c} and B = {10, 20, 30} then A≈B but A≠B.
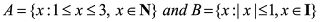then A≈B but A≠B.- { x : x2 –16 = 0, } and B =
{x : x–16=0, } then A≈B as well as A = B.
SUBSETS
If every element of a set A is also an element of a
set B, then A is called a subset of B or A is contained in B and we write AϹB. [The symbol Ϲis read as “a subset of” or
“contained in”]
Thus AϹB if x ∈ A ⇒ x ∈ B
If AϹB, then we also say that B
is a SUPERSET of A and we write BϽA (read as "B contains
A").
THEOREMS
·
i.e. null set is subset of every set
·
i.e. every set is subset of itself
For any set A, φ and A are called IMPROPER SUBSETS.
All other subsets of A are called PROPER SUBSETS. If B is a proper subset of A,
we write BϹA. [The symbol Ϲ is read as “ is a proper subset
of”]
[The symbol ↔is read as “if and only if”
also written as iff or sometimes “implies and implied by”]
- A finite set containing n elements has
2n subsets. However the number of proper subsets is 2n –
2.
Examples :
- If A = {2, 3, 4} and B = {1, 2, 3, 4],
then
- If A = {a, b, c} then n (A) = 3. Hence
A has 23 = 8 subsets, viz, φ; {a}; {b}; {c}; {a, b}; {b, c}; {c, a};
{a, b, c}. φ and {a,b, c} = A are improper subsets. All other are proper
subsets
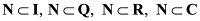
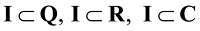
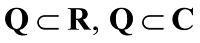
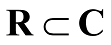
- The set of irrational numbers, denoted
by T, is composed of all other real numbers. Thus T = {x : x ∈ R and x ∉ Q}, i.e., all real numbers that are
not rational. Some of the obvious relations among these subsets
are: N ⊂ Ζ ⊂ Q, Q ⊂ R, T ⊂ R, N ⊄ Τ.
INTERVALS AS SUBSETS OF R
Let a, b ∈ R and a < b. Then
the set of real numbers {y : a < y < b}
is called an open interval and is denoted by (a, b). All the points
between a and b belong to the open interval (a, b) but a, b themselves do not
belong to this interval.
The interval which contains the end points also is
called closed interval and is denoted by [a, b]. Thus [a, b] = {x : a ≤
x ≤ b}.
We can also have intervals closed at one end and open at the other, i.e.
[a, b) = {x : a ≤ x < b} is an open interval from a to b, including a but excluding b.
(a, b] = {x : a < x ≤ b} is an open interval from a to b including b but excluding a.
These notations provide an alternative way of designating the subsets of set of real numbers. For example, if A = (–3, 5) and B = [– 7, 9], then A ⊂ B. The set [0, ∞) defines the set of non-negative real numbers, while set (– ∞, 0) defines the set of negative real numbers. The set (-∞, ∞) describes the set of real numbers in relation to a line extending from -∞ to ∞.
On real number line, various types of intervals described above as subsets of R, are shown in the following figure :
Here, we note that an interval contains infinitely many points.
For example, the set {x : x ∈ R, – 5 < x ≤ 7}, written in set-builder form, can be written in the form of interval as (–5, 7] and the interval [– 3, 5) can be written in set-builder form as {x : – 3 ≤ x < 5}.
The number (b – a) is called the length of any of the intervals (a, b), [a, b], (a, b] or [a, b). The intervals (a, b] and [a, b) are also referred as semi-closed (or semi-open) intervals.
POWER SET
Let A is a given set. The collection of all the subsets of the set A is called the power set of A. It is denoted by P(A).
Hence, P(A) = {S : S
A}
For example : If A = {a, b, c} then
P(A) = {φ, {a}, {b}, {c}, {a,b} {b,c} {c,a} {a, b, c}}
Clearly if A is a finite set and n(A) = m, then n (P(A)) = 2m
UNIVERSAL SET
A set, which contains all sets under consideration as subsets is called the universal set. It is denoted by U. The choice of universal set is not unique. Different universal sets are used in different contexts.
COMPARABLE SETS
Two sets A and B are said to be comparable if 
.
VENN DIAGRAM
Most of the relationship between sets can be represented by means of diagrams called Venn diagrams. In the Venn diagram the universal set U is represented by the interior of a rectangle. Other sets under consideration are represented by the interior of circles drawn inside the rectangle. If a set A is a subset of a set B then the circle representing A is drawn inside the circle representing B.
OPERATIONS
ON SETS
UNION
OF SETS
Let A and B be two sets. The union of A and B is the set of all those elements which belong to A or B or A and B both. Symbolically we write A∪B which is read as “A union B” Thus
A∪B = {x : x
A or x
B} or x A∪B x A or x B Also, 
In the Venn diagrams the shaded regions represent the union of sets A and B in different cases
The union of a number of sets A1, A2, A3, .........An, i.e. A1∪A2∪A3∪.......∪An is represented by
For example :
If A = {1,2,3}; B={2,3,4,5}. Then A ∪ B = {1,2,3,4,5}
If A = {a, e,i,o,u}; B= {e,o,u}. Then A ∪ B = {a, e,i,o,u}
If A = {1,2}; B = {a,b,c} Then A ∪ B = {1,2,a,b,c}
If A {x : x ∈ I+}; B{x : x ∈ I and x < 0} ;
Then A ∪ B { ..........4, 3, 2, 1, -1, -2, -3,....} = 
ALGEBRA OF UNION
Let A, B, C be any three sets defined in the universal set U, then
Idempotent Law : A ∪ A = A
Commutative Law : A ∪ B = B ∪ A
Associative Law : (A ∪ B) ∪ C = A ∪ (B ∪ C)
Identity Law : (i) A ∪ φ = A, (ii) A ∪ U = U
INTERSECTION
OF SETS
Let A and B are two sets. The intersection of the sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write A∩B, which is read as “A intersection B” Thus, A ∩ B = {x : x ∈ A and x ∈ B} or x ∈ A ∩ B ⇒x ∈ A and x ∈ B
Also, 
. In the following Venn diagrams, the shaded regions represent the intersection of sets A and B in different cases.
The intersection of a number of sets A1, A2, A3, ....., An i.e. A1∩ A2∩ A3∩..............∩ An is represented by 
.
For example :
If A = {2,4,7,10} and B = {1, 2, 3, 4}, Then A∩B = {2,4}
If A = {x : x is a prime number} and B = {x : x ∈ N}
Then A∩B = {x : x is a prime number} = A. [Note that A ⊂ B]
If A = {1,3,5,7,9,......}; B = {2,4.6,8,.....}, Then A ∩ B = φ.
ALGEBRA OF INTERSECTION
Idempotent Law : A∩A = A
Commutative Law : A∩B = B∩A
Associative Law : (A∩B)∩C = A∩ (B∩C)
Identity Law : (i) A∩φ = φ, (ii) A∩U = A
Distributive law : (i) A∪(B∩C) = (A∪B) ∩ (A∪C) (ii) A∩(B∪C) = (A∩B) ∪ (A∩C)
DIFFERENCE
OF SETS
Let A and B are two sets. The difference of the sets A and B, in this order, is the set of elements which belong to A but not to B. Symbolically, we write A – B and read as “ A difference B” Thus, A – B = { x : x ∈ A and x ∉ B}. Similarly, B – A = { x : x ∈ B and x ∉ A}. In the Venn diagram, A – B and B – A are shown by shaded regions.
For example :
If A = { 1, 2, 3, 4} and B = { 3, 4, 5, 6}, Then A – B = {1, 2} and B – A = {5, 6}. We note that A – B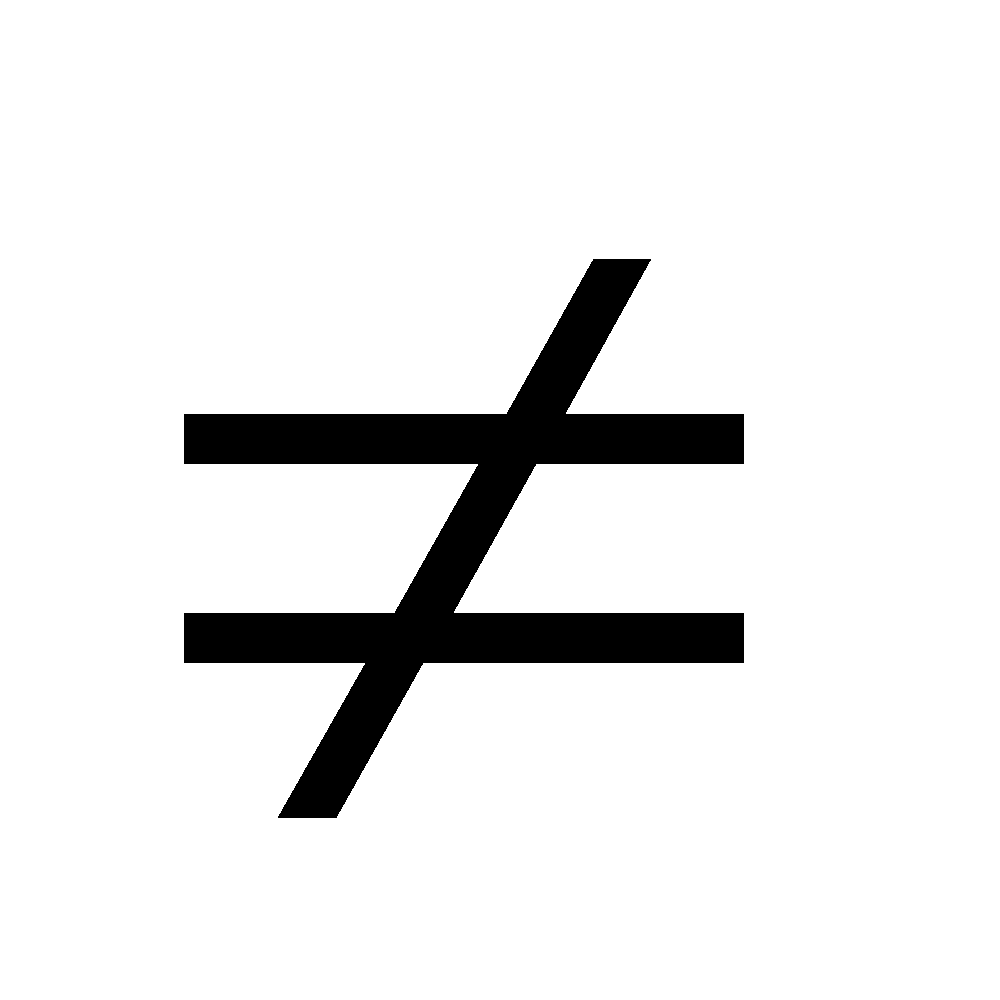 
B – A Notes:
A⊆A∪B
B ⊆ A ∪ B
A∩B⊆A
A∩B⊆B
If A⊆B, then (a) A∪B = B, (b) A∩B = A
If A∩B = φ, then A and B are called DISJOINT SETS
If A∩B ≠ φ, then A and B are called OVERLAPPING SETS.
A – B⊆A, B – A ⊆ B
A⊆BA – B = φ
A – B ≠ B – A
A – B = A – (A∩B)
A – φ = A and A – A = φ
A – (A – B) = A B
A – B = B – A A = B
A – B, B – A, A∩B are pairwise disjoint.
SYMMETRIC
DIFFERENCE
If A and B are two sets, then the set, (A – B) ∪ (B – A) is called the symmetric difference of A and B and is denoted by A Δ B or A ⊕B
∴ A Δ B = {x : x ∈ A and x ∉B or x ∈ B and x∉A} = {x : x∉A∩B}
In the Venn diagram the shaded area represents A Δ B
For example :
Let A = {1, 2, 3} and B = {2, 3, 4, 5} then
A – B = {1} and B –A = {4,5}
∴ A Δ B = (A–B) ∪ (B–A) = {1, 4, 5}
COMPLEMENT OF A SET
Let U be the universal set and A is a subset of U. The complement of the set A, denoted be A’ or Ac is the set of all those elements of U which are not the elements of A.
Thus, A’ or Ac = { x : x ∈ U and x ∉A} = U – A
∴ x ∈ A’ ⇔ x∉A
The complement of the set A is shown by shaded area in the following Venn diagram.
ALGEBRA OF COMPLEMENT
A∩A’ = φ
A ∪ A’ = U
U’ = φ
φ’ = U
(A’)’ = A
A ⊆ B ⇔ B’ ⊆ A’
A – B = A∩B’
B – A = B∩A’
A – B = B’ – A’
De morgan’s laws
SOME IMPORTANT RESULTS
A Δ B = (A–B) ∪ (B–A) = (A∪B) – (A∩B)
A – B = A ⇔ A ∩ B = φ
(A–B) ∪ B = A∪B
(A – B) ∩ B = φ
A ∩ (B – C) = (A∩B) – (A∩C)
A ∩ (BΔC) = (A ∩ B) Δ (A∩C)
(5) and (6) do not hold for union of sets.
, where P(A) is the power set of A
VERY IMPORTANT THEOREMS ON CARDINAL NUMBERS
Let A, B, C are finite sets in a finite universal set U. Then
n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
n (A ∪ B) = n(A) + n (B) 
A and B are disjoint non void sets. n (A∪B∪C) = n (A) + n (B) + n (C) – n (A∩B) – n (B∩C) – n (C∩A) + n ( A∩B∩C)
The results (1) and (3) can be extended to any number of sets.
n (A–B) = n (A) – n (A ∩ B) = n (A ∩ B’)
n (A Δ B) = n (A) + n (B) – 2 n (A∩B)
n(A’) = n (U) – n (A)
n (A’∪B’) = n (U) – n (A∩B)
n (A’∩B’) = n (U) – n (A∪B)
Let n (A) = p and n (B) = q
Then min {n(A∪B)} = max {p,q} and
max {n (A∪B)} = p + q
min { n (A∩B)} = 0 and max {n (A∩B)} = min {p, q}
If A1, A2, ......, Am are disjoint sets, then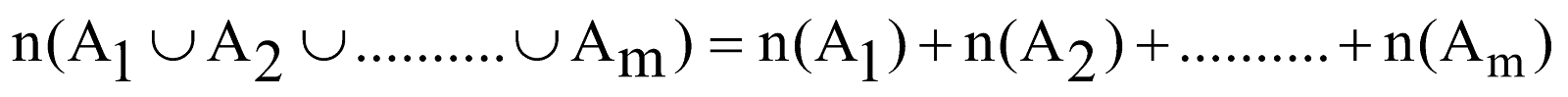 
CARTESIAN PRODUCT OF SETS
Ordered Pair : A pair of objects, listed in a specific order, is called an ordered pair, for example (a, b) is an ordered pair of two elements a and b, a is called the FIRST ELEMENT and b, the SECOND ELEMENT.
Two ordered pairs (a, b) and (c, d) are equal if any only if a = c and b = d.
Cartesian product of Sets : Let A and B are two non-empty sets. The set of all ordered pairs (a, b) of elements a ∈ A and b ∈ B is called the Cartesian product of sets A and B and is denoted by A × B. Thus A × B = {(a, b) : a ∈A, b ∈ B}
For example :
If A = {1, 2, 3} and B = {a, b}, then
A × B = {(1, a)}, (1, b), (2, a), (2, b), (3, a), (3, b)}
B × A = {(a, 1)}, (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)}
A × A = {(1, 1)}, (1, 2), (1, 3), (2, 1), (2, 2), (2, 3),(3, 1), (3, 2), (3, 3)}
B × B = { (a, a), (a, b), (b, a) (b, b)}
Note :
If at least one of A or B is empty set then A×B = φ
A × B ≠ φ iff A ≠ φ and B ≠ φ
In general A × B ≠ B × A
If A and B are finite sets, then n (A×B) = n (A). n (B)
If A and B are non-empty sets and either A or B is an infinite set, then A×B is an infinite set
If A = B, then A×B is expressed as A2. Thus A2 = A×A
We can also define, in a similar way, ordered triplets. If A, B, and C are three sets, then (a, b, c), where a ∈A, b ∈ B and c ∈ C, is called an ordered triplet. The Cartesian product of sets A, B and C is defined as
A × B × C = {(a, b, c,) : a ∈ A, b ∈ B, c ∈ C}.
An ordered pair and ordered triplet are also called 2-tuple and 3-tuple, respectively. In general, if A1, A2,.....An are n sets, then (a1, a2,........an) is called an n-tuple where. ai∈Ai, i = 1, 2......., n and the set of all such n-tuples, is called the Cartesian product of A1, A2, .......An. It is denoted by A1×A2×........×An. Thus
A1×A2×.....×An = {(a1, a2,........an) : ai∈Ai, 
}.
SOME IMPORTANT THEOREMS
A × (B∪C) = (A×B) ∪ (A×C)
A×(B∩C) = (A×B) ∩ (A×C)
A× (B–C) = (A×B) – (A×C)
If A and B are two non-empty sets, then A×B = B×A ⇔ A=B
If A ⊆ B, then A×A ⊆ (A×B) ∩ (B×A)
A⊆ B ⇒A × C ⊆ B×C for any set C
A ⊆ B and C⊆ D ⇒ A×C ⊆ B × D
(A×B) ∪ (C×D) ⊆ (A∪ C)×(B∪D)
(A×B) ∩ (C×D) = (A∩C) × (B∩D)
(A×B) ∩ (B×A) = (A∩B) × (B∩A)
Let A and B be two non-empty sets having n elements in common, then A×B and B×A have n2 elements in common.
RELATIONS
Let A and B be two non-empty sets. Then a relation (BINARY RELATION) R from A to B is a subset of A×B. That is, R is a relation from A to B ⇔ R⊆A × B
If R ⊆ A×A, the R is said to be a relation on A.
If (a, b) ∈R, then we write aRb and we say a is R related to b. Thus, (a, b) ∈R ⇔ aRb.
If 
, then we say that a is not related to b.
Example :
If A = {3, 5} and B = {2, 4}, then A× B = {(3,2), (3,4), (5,2), (5,4)}
Let R be a relation “is greater than” from A to B,
That is aRb ⇔ a > b, a ∈ A, b ∈ B
Then, 3R2, 5R2, 5R4
∴ R = {(3,2), (5,2), (5,4)}. Clearly 
The visual representation of a relation is an arrow diagram as shown below:
If A = {2, 3, 5, 6} and R be a relation “divides” on A that is aRb ⇔ a divides b then 2R2, 2R6, 3R3, 3R6, 5R5, 6R6
∴ R = {(2,2), (2,6), (3,3), (3,6) (5,5) (6,6} ⊆ A×A
The corresponding arrow diagram is as follows :
DOMAIN AND RANGE OF A RELATION
Radius of nucleus.
-particles
